Is Clustering Machine Learning?

Cluster analysis is an algorithm that enables the extraction of meaningful insights from large datasets without the need for labeled information. At its core, clustering involves the grouping of similar data points into distinct clusters based on various criteria, such as proximity or similarity measures like Euclidean distance. From customer segmentation to anomaly detection, clustering methods like K-means, agglomerative clustering, and density-based approaches play a fundamental role in uncovering hidden patterns and structures within unlabeled data. As data scientists and machine learning engineers navigate the clustering algorithms and techniques, understanding the nuances of centroid-based and distribution-based methods becomes the prerequisite to achieving optimal clustering results.

Is Clustering a Machine Learning Algorithm?

First, let’s answer the question.

Yes, clustering is often categorized as a machine learning technique, specifically falling under the domain of unsupervised learning. While supervised learning algorithms require labeled data for training, unsupervised learning algorithms like clustering operate on unlabeled datasets, autonomously identifying patterns, structures, or groups within the data.

Clustering algorithms aim to partition the data into subsets, or clusters, where data points within the same cluster are more similar to each other compared to those in different clusters. These algorithms use various criteria, such as distance measures or density-based approaches, to group data points together.

Although clustering itself does not involve predicting labels or outcomes like many traditional supervised learning algorithms, it still involves learning patterns or structures from data, which aligns with the broader definition of machine learning. Therefore, while clustering may not fit the conventional understanding of machine learning as predictive modeling, it is indeed a vital component of the machine learning toolkit, particularly in scenarios where understanding the inherent structure of unlabeled data is essential.

Understanding Clustering in Data Science and Machine Learning

Clustering, a fundamental concept in data science and machine learning, involves the grouping of data points into distinct clusters based on their inherent similarities. It serves as a tool for finding hidden patterns, structures, or relationships within large, unlabeled datasets. Here’s an overview of its significance, methods, and key concepts:

Importance of Clustering

Pattern Recognition: Clustering aids in identifying patterns or structures within data, facilitating insights and decision-making.
Data Exploration: It enables exploration and understanding of complex datasets by organizing them into meaningful groups.
Unsupervised Learning: Clustering falls under the domain of unsupervised learning, where algorithms learn from data without explicit labels, making it valuable for scenarios with limited labeled data.

Overview of Different Clustering Methods

Clustering methods can be broadly categorized into various approaches, each with its unique characteristics and applications:

Centroid-Based Clustering: Algorithms such as K-means clustering partition data into clusters around central points called centroids.
Density-Based Clustering: Methods like DBSCAN identify clusters based on regions of high data point density, allowing for the detection of arbitrary shape clusters.
Hierarchical Clustering: This approach constructs a tree-like hierarchy of clusters, offering insights into both individual data points and broader cluster structures.
Distribution-Based Clustering: Techniques like Gaussian Mixture Models model clusters as probability distributions, accommodating clusters with different shapes and sizes.

Key Concepts and Terms

Cluster Center/Centroids: Representative points within clusters, often used to characterize the cluster’s properties.
Cluster ID: Unique identifiers assigned to individual clusters for reference and analysis.
Similarity Measure: Metrics used to quantify the similarity between data points, guiding the clustering process.
Optimal Number of Clusters: Determining the ideal number of clusters for a given dataset, often addressed through methods like the elbow method or silhouette analysis.

Clustering methods, with their diverse approaches and applications, play a pivotal role in various fields such as market segmentation, anomaly detection, and recommendation systems. By efficiently organizing data into meaningful groups, clustering enhances data analysis and drives informed decision-making in data-driven industries.

Clustering serves as a cornerstone in the realm of unsupervised learning, empowering data scientists to extract valuable insights from unlabeled datasets. With its array of methods and concepts, clustering remains a vital tool for understanding complex data structures and uncovering hidden patterns, contributing significantly to the advancement of data science and machine learning.

What is Cluster Analysis?

Cluster analysis, or clustering, is the process of organizing a set of objects into groups, or clusters, such that objects within the same cluster are more similar to each other than those in other clusters. The primary goal is to uncover hidden patterns or structures within the data, without prior knowledge of group labels. Clustering is widely used across diverse fields, including data mining, social network analysis, and market segmentation, among others.

Explanation of Unsupervised Learning and its Relevance to Clustering

Unsupervised learning is a branch of machine learning where algorithms learn patterns from unlabeled data. Unlike supervised learning, which requires labeled examples, unsupervised learning algorithms extract information from input data without explicit guidance. Clustering, as an unsupervised learning technique, plays a crucial role in organizing and understanding large, unlabeled datasets by identifying inherent structures or groups.

Types of Clustering Techniques

Centroid-based Clustering: Algorithms such as K-means partition the data into K clusters, with each cluster represented by a centroid or center point. Data points are assigned to the nearest centroid based on distance metrics such as Euclidean or Manhattan distance.
Density-based Clustering: Density-based techniques, like DBSCAN, identify clusters based on regions of high data point density. Data points within dense regions are considered part of the same cluster, while those in sparse areas are labeled as noise.
Distribution-based Clustering: Distribution-based methods, such as Gaussian Mixture Models (GMM), model clusters as probability distributions. Each cluster is represented by a probability distribution, allowing for the detection of clusters with different shapes and sizes.
Hierarchical Clustering: Hierarchical clustering constructs a tree-like hierarchy of clusters, where clusters at higher levels encapsulate smaller clusters or individual data points. This approach provides insights into both individual data points and broader cluster structures.

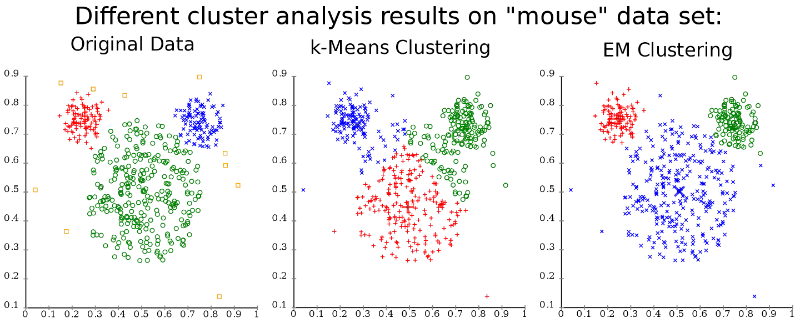
Key Terms and Concepts

Cluster Centroids: Representative points within clusters, often used to characterize the cluster’s properties.
Similarity Measure: Metrics used to quantify the similarity between data points, guiding the clustering process.
Cluster ID: Unique identifiers assigned to individual clusters for reference and analysis.
Number of Features: The dimensions or attributes used to describe each data point, influencing clustering results and performance.

Clustering includes various techniques for unsupervised learning, allowing for the identification of hidden structures within unlabeled data. By leveraging different approaches and concepts, clustering techniques enable efficient data organization, pattern recognition, and insight generation in data science and machine learning applications.

Popular Clustering Algorithms

Clustering algorithms are essential tools in unsupervised learning, offering insights into the inherent structures of data. This section explores three popular clustering algorithms: K-means clustering, Agglomerative clustering, and DBSCAN.

K-means Clustering

Overview and Working Principle

K-means clustering is a centroid-based algorithm that partitions data into K clusters, where K is predetermined. The algorithm iteratively assigns data points to the nearest cluster centroid and updates the centroids based on the mean of the data points assigned to each cluster. This process continues until convergence, where centroids no longer change significantly.

Steps Involved in the K-means Algorithm

Initialization: Randomly select K initial centroids from the dataset.
Assignment: Assign each data point to the nearest centroid based on distance metrics like Euclidean distance.
Update: Recalculate the centroids as the mean of all data points assigned to each cluster.
Repeat: Iterate steps 2 and 3 until convergence criteria are met.

Application Areas and Common Use Cases

Customer Segmentation: Dividing customers into distinct groups based on purchasing behavior or demographics.
Market Analysis: Analyzing market trends and segmenting customers for targeted marketing campaigns.

Agglomerative Clustering

Explanation of the Algorithm

Agglomerative clustering is a hierarchical clustering algorithm that starts with each data point as its own cluster and merges clusters iteratively based on a distance measure until only one cluster remains. The algorithm forms a hierarchy of clusters, resulting in a tree-like structure known as a dendrogram.

Hierarchical Nature and Tree-like Structure

Agglomerative clustering exhibits a hierarchical nature, where clusters are successively merged based on similarity, forming a tree-like structure. This structure provides insights into both individual data points and broader cluster relationships.

Comparison with Other Clustering Methods

Compared to centroid-based methods like K-means, agglomerative clustering does not require specifying the number of clusters beforehand. Additionally, it can handle non-convex shapes and clusters of varying sizes more effectively.

DBSCAN (Density-Based Spatial Clustering of Applications with Noise)

How it Works and its Advantages

DBSCAN identifies clusters based on regions of high data point density, ignoring areas with low density. It requires two parameters: epsilon (ε), defining the maximum distance between two points to be considered neighbors, and minPoints, specifying the minimum number of points required to form a dense region.

Handling Arbitrary Shape Clusters and Noise

DBSCAN can handle clusters of arbitrary shapes and sizes and is robust to noise and outliers. It identifies clusters as dense regions separated by areas of lower density, making it suitable for datasets with irregular shapes and noise.

Real-World Applications

Anomaly Detection: Identifying unusual patterns or outliers in data, such as fraudulent transactions.
Social Network Analysis: Discovering communities or groups within social networks based on connectivity patterns.

These popular clustering algorithms offer diverse approaches to unsupervised learning, catering to different data characteristics and application scenarios. Whether it’s the simplicity of K-means, the hierarchical structure of agglomerative clustering, or the robustness of DBSCAN, each algorithm contributes to the exploration and understanding of complex datasets.

Evaluating Clustering Results

Evaluating clustering results is crucial to assess the quality and effectiveness of clustering algorithms. This section discusses metrics for assessing clustering quality and the challenges and limitations associated with clustering algorithms.

Metrics for Assessing Clustering Quality

1. Elbow Method for Determining the Optimal Number of Clusters

The elbow method is a graphical approach used to determine the optimal number of clusters in a dataset. It involves plotting the within-cluster sum of squares (WCSS) against the number of clusters and identifying the “elbow point,” where the rate of decrease in WCSS slows down significantly. The number of clusters at the elbow point is often considered the optimal choice.

2. Silhouette Score and Other Evaluation Metrics

The silhouette score measures the cohesion and separation of clusters. It calculates the mean silhouette coefficient for all data points, where higher values indicate better-defined clusters. Other evaluation metrics include Dunn index, Davies–Bouldin index, and Rand index, each offering insights into different aspects of clustering quality.

Challenges and Limitations of Clustering Algorithms

1. Sensitivity to Initial Conditions (e.g., K-means)

Many clustering algorithms, such as K-means, are sensitive to initial cluster centroids. Different initializations can lead to different clustering results, impacting the stability and reliability of the algorithm. Multiple runs with random initializations are often required to mitigate this issue.

2. Difficulty in Handling High-Dimensional Data

Clustering algorithms may struggle with high-dimensional data due to the curse of dimensionality. As the number of features increases, the distance between data points becomes less meaningful, leading to challenges in defining meaningful clusters. Dimensionality reduction techniques, such as PCA or t-SNE, can be employed to address this issue.

3. Impact of Outliers and Noisy Data Points

Outliers and noisy data points can significantly affect clustering results by distorting cluster boundaries and influencing centroid positions. Density-based clustering methods like DBSCAN are more robust to outliers, while centroid-based algorithms like K-means may produce suboptimal results in the presence of outliers. Preprocessing techniques like outlier removal or noise reduction can help mitigate these effects.

Evaluating clustering results involves assessing clustering quality using various metrics and understanding the challenges and limitations associated with clustering algorithms. By employing appropriate evaluation techniques and addressing inherent limitations, data scientists can ensure the reliability and effectiveness of clustering outcomes in data analysis and decision-making processes.

Practical Considerations in Clustering

Clustering, while a powerful tool in data analysis, requires careful consideration of various practical aspects to ensure accurate and meaningful results. This section explores key considerations in the practical application of clustering algorithms.

Data Preparation and Preprocessing Steps

Data Cleaning: Remove missing values, handle outliers, and address inconsistencies in the data to ensure quality inputs for clustering algorithms.
Feature Selection: Identify relevant features and eliminate irrelevant or redundant ones to improve clustering performance and reduce computational complexity.
Normalization: Scale the data to a consistent range to prevent features with larger magnitudes from dominating the clustering process.
Dimensionality Reduction: Reduce the dimensionality of the dataset using techniques like PCA or t-SNE to improve clustering performance, especially with high-dimensional data.

Choosing the Right Clustering Algorithm for the Dataset

Understand Data Characteristics: Assess the nature of the dataset, including its size, dimensionality, and distribution, to select an appropriate clustering algorithm.
Consider Algorithm Assumptions: Choose algorithms that align with the assumptions and characteristics of the data, such as the presence of noise, outliers, or non-linear relationships.
Experimentation and Evaluation: Experiment with different clustering algorithms and evaluate their performance using appropriate metrics to identify the most suitable approach for the dataset.

Handling Large Datasets and Scalability Issues

Sampling: Consider sampling techniques to reduce the size of large datasets while preserving the underlying structure and patterns.
Parallelization: Utilize parallel processing or distributed computing frameworks to enhance the scalability of clustering algorithms and handle large volumes of data efficiently.
Incremental Learning: Implement incremental learning approaches to process data in batches and update clustering models iteratively, reducing memory requirements and computational overhead.

Dimensionality Reduction Techniques for Improving Clustering Performance

Principal Component Analysis (PCA): Reduce the dimensionality of the dataset by transforming features into a lower-dimensional space while preserving the variance.
t-Distributed Stochastic Neighbor Embedding (t-SNE): Visualize high-dimensional data in a lower-dimensional space, facilitating cluster identification and interpretation.
Autoencoders: Use neural network-based techniques to learn compact representations of high-dimensional data, aiding in dimensionality reduction and feature extraction for clustering.

Effective clustering requires careful consideration of practical aspects such as data preparation, algorithm selection, scalability, and dimensionality reduction. By addressing these considerations thoughtfully, data scientists can enhance the quality and efficiency of clustering outcomes, enabling valuable insights and knowledge discovery from complex datasets.

Clustering Applications and Use Cases

Clustering algorithms find wide-ranging applications across various domains, enabling data-driven insights and decision-making. This section explores some of the key applications and use cases of clustering.

Market Segmentation and Customer Behavior Analysis

Market Segmentation: Clustering techniques are employed to divide customers into distinct segments based on similarities in demographics, purchasing behavior, or preferences.
Customer Behavior Analysis: Clustering helps identify patterns and trends in customer behavior, enabling businesses to tailor marketing strategies and offerings to specific customer segments.

Recommendation Systems and Personalized Content Delivery

Recommendation Systems: Clustering is used to group users with similar preferences or interests, allowing recommendation systems to suggest relevant products, services, or content.
Personalized Content Delivery: Clustering helps personalize content delivery by categorizing users into clusters and delivering content that aligns with their preferences and interests.

Anomaly Detection and Fraud Prevention

Anomaly Detection: Clustering techniques aid in identifying unusual patterns or outliers in data, such as fraudulent transactions or abnormal behavior, by separating anomalous data points from normal ones.
Fraud Prevention: Clustering enables the detection of fraudulent activities by identifying clusters of transactions or behaviors that deviate from typical patterns, allowing for timely intervention and prevention of fraudulent activities.

Pattern Recognition and Data Compression

Pattern Recognition: Clustering algorithms are used to identify and extract patterns or structures within data, facilitating pattern recognition tasks in various domains such as image processing, speech recognition, and natural language processing.
Data Compression: Clustering helps compress large volumes of data by representing clusters with fewer parameters, reducing storage space and computational complexity while retaining essential information.

Clustering algorithms play a pivotal role in diverse applications such as market segmentation, recommendation systems, anomaly detection, and pattern recognition. By leveraging clustering techniques, organizations can gain valuable insights from data, improve decision-making processes, and enhance user experiences across various domains.

Future Directions and Conclusion

As clustering continues to evolve, it presents exciting opportunities and challenges in advancing data science and machine learning. This section explores emerging trends, integration with other techniques, potential applications, and concluding thoughts on the role of clustering.

Emerging Trends in Clustering and Unsupervised Learning

Deep Learning Integration: The integration of clustering with deep learning techniques holds promise for enhancing clustering performance, especially in complex data domains.
Graph-based Clustering: Graph-based clustering methods are gaining traction, offering efficient solutions for clustering data with complex relationships or network structures.
Streaming and Online Clustering: With the increasing volume and velocity of data, there is a growing need for streaming and online clustering algorithms capable of processing data in real-time.

Integration of Clustering with Other Machine Learning Techniques

Deep Learning: Deep learning models can be integrated with clustering algorithms to enhance feature representation and clustering performance, especially in high-dimensional data spaces.
Reinforcement Learning: Reinforcement learning algorithms can be combined with clustering to optimize clustering objectives and adapt clustering decisions based on feedback.

Potential Applications in Various Industries and Domains

Healthcare: Clustering techniques can aid in patient stratification, disease subtype identification, and drug discovery.
Finance: Clustering algorithms can be utilized for fraud detection, risk assessment, and portfolio optimization.
Smart Cities: Clustering methods can help analyze urban data for traffic management, resource allocation, and infrastructure planning.

Conclusion

Clustering holds immense potential in shaping the future of data science and machine learning, offering solutions to a wide array of challenges and opportunities across various industries and domains. As researchers and practitioners continue to explore new methodologies, algorithms, and applications, clustering will continue to evolve, driving advancements in unsupervised learning and contributing to the advancement of data-driven decision-making.